機械学習における説明変数の選択にSHAPを使ってみた

前回に引き続いて機械学習における変数選択を実行するにあたって役に立つライブラリを紹介する。SHAPは、ゲーム理論に基づいて説明変数に意味を与えることを目的として開発されたものであるが、変数選択に用いることもできる。今回sklearnにあるアヤメ(iris)のデータを用いて試してみた。

まずは単純にアヤメのデータを読込んで、目的変数をSepal Length(がくの長さ)として、それ以外の変数で目的変数を予測するモデルを作成した。setosa, virginica等の種類についてはOne Hotベクトルとして、回帰方法は単純な線形回帰とした。まず下のコードはDataFrameを生成するまで。

import pandas as pd
import numpy as np
from sklearn import linear_model
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
iris = load_iris()
from sklearn.metrics import mean_absolute_error, r2_score
from sklearn.model_selection import train_test_split
import shap
import xgboost as xgb
from sklearn.ensemble import RandomForestRegressor
from boruta import BorutaPy

shap_threshold = 0.05

# データフレーム作成
df = pd.DataFrame(iris.data, columns = ['Sepal Length(cm)', 'Sepal Width(cm)', 'Petal Length(cm)', 'Petal Width(cm)'])

続いてOne Hotベクトルでアヤメの種類を数値にする処理が下のコードとなる。One Hot化にはPandasのget_dummiesメソッドを使用した。

# irisの種類をデータフレームに追加する
target=iris['target']
target_names=iris['target_names']
name=target_names[target]
df["Name"] = pd.Series(name)
df = pd.get_dummies(df)

y = df[["Sepal Length(cm)"]]
x = df.drop('Sepal Length(cm)', axis= 1)

x_train, x_test,y_train, y_test = train_test_split(x, y, random_state=0)

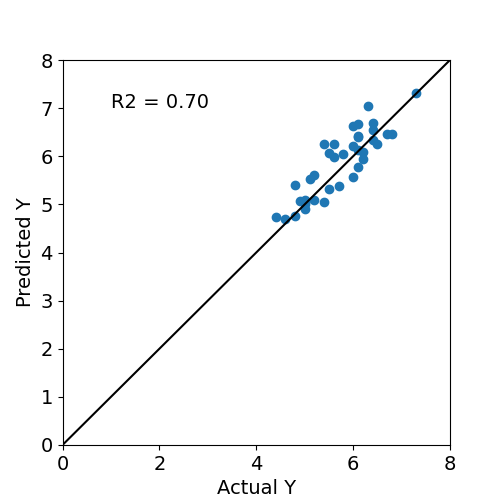
次に線形回帰モデルを作って回帰した結果の図を作成するコードが下で、その下に実際の図を張り付けた。決定係数は0.70とそれなりの精度で予測できている。

# 線形回帰モデルを生成し、回帰
linear_regressor  = linear_model.LinearRegression()
linear_regressor.fit(x_train, y_train)
y_predict = linear_regressor.predict(x_test)

print("Coefficients: \n", linear_regressor.coef_)
# The mean squared error
print("MAE: %.2f" % mean_absolute_error(y_test, y_predict))
# The coefficient of determination: 1 is perfect prediction
print("R2: %.2f" % r2_score(y_test, y_predict))

# plt.figure()
plt.rcParams['font.size'] = 14
plt.figure(figsize=(5, 5))
plt.scatter(y_test, y_predict)
plt.ylim(0, 8) # Y のサイズ
plt.xlim(0, 8) # X のサイズ
plt.plot([0, 8], [0, 8], 'k-')
plt.xlabel('Actual Y') 
plt.ylabel('Predicted Y') 
plt.text(1,7, 'R2 = %.2f' % r2_score(y_test, y_predict), fontsize= 14)
plt.show()

これに対して、説明変数の重要度をSHAPで計算させてみた結果が下となる。Sepal Lengthに影響するのは主にPetal WidthとPetal Lengthで、Sepal Widthはあまり影響しないというちょっと意外な結果となる。

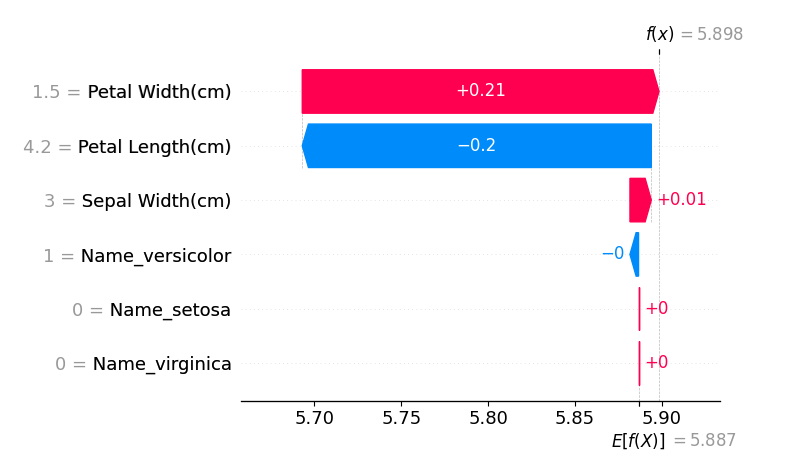
SHAPの計算結果を元に説明変数を選択するコードが下の部分となる。SHAPの計算結果から重要度を計算し、その重要度がある閾値(今回は0.05)を超えたものを採用するロジックとなっている。

# SHAPで説明変数を絞る
model1 = xgb.XGBRegressor().fit(x_train, y_train)
explainer = shap.Explainer(model1)
shap_values = explainer(x_train)
shap.plots.waterfall(shap_values[0])

df_shap_values = pd.DataFrame(data=shap_values.values,columns=x_train.columns)
df_feature_importance = pd.DataFrame(columns=['feature','importance'])
for col in df_shap_values.columns:
    importance = df_shap_values[col].abs().mean()
    df_feature_importance.loc[len(df_feature_importance)] = [col,importance]
df_feature_importance = df_feature_importance.sort_values('importance',ascending=False)

effective_desc_df = df_feature_importance.loc[df_feature_importance['importance'] > shap_threshold]
effective_desc_col = effective_desc_df['feature'].values.tolist()

eff_df = df.loc[:, effective_desc_col]

このようにして説明変数を選択して、更に説明変数間の自乗項と交差項を入れて、Borutaで説明変数を絞り込む、という操作を加えた。Borutaについては、説明変数を選択するライブラリとしてよく使用されているので使用方法は省略する。

SHAPとBorutaで絞り込んだ説明変数を用いて、前と同様に線形回帰してみた。その結果が下の図となる。

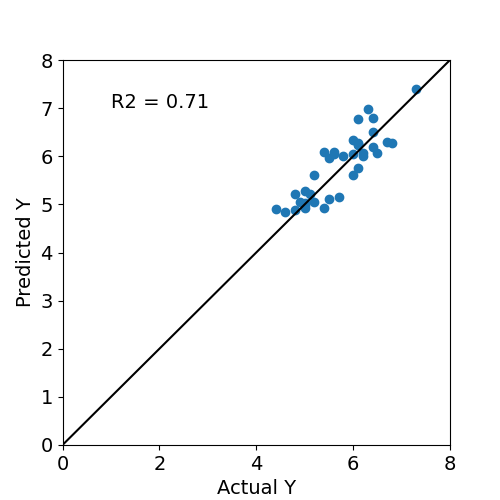
決定係数は0.71と単純な線形回帰よりも0.01だけ良くなったものの、殆ど変化しなかった。今回の系に対しては影響の大きな因子が2つ(Petal LengthとPetal Width)のみで他の影響が小さいため、どのように選択しても影響の大きな因子が支配的になるためと思われる。

実際に問題とされるような、より複雑な系に対してはこのような手法が効果を発揮する可能性がある。継続して色々と試してみようと思っている。

#SHAP #Boruta #機械学習

機械学習における説明変数の選択(2)

コメント